Simulate Regular Expressions Through A Program In Haskell Assignment Solution

Instructions

Objective

Write a Haskell assignment program that allows users to simulate regular expressions.

Requirements and Specifications

• Define string containing regular expressions for the following languages over the alphabet {a,b,c}.

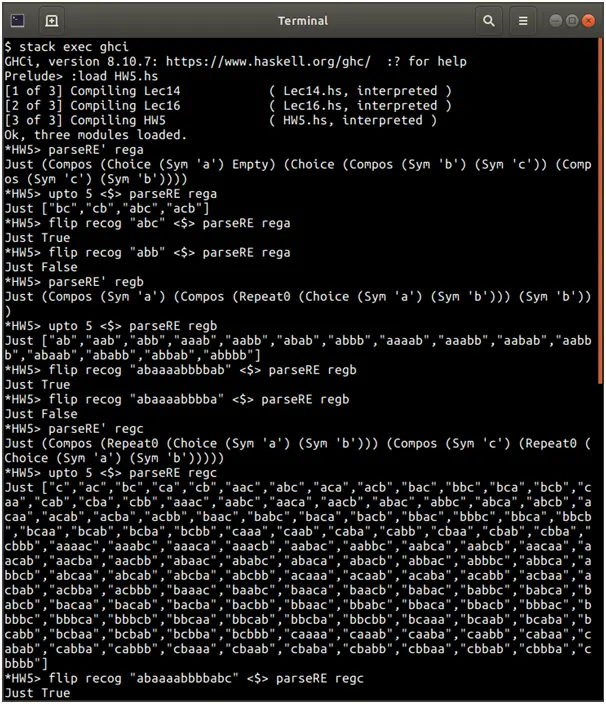
-- A. The language {"bc","cb","abc","acb"}

-- B. Strings that begin with 'a' and end with 'b' and do not contain 'c'

-- C. Strings in which 'c' occurs exactly once

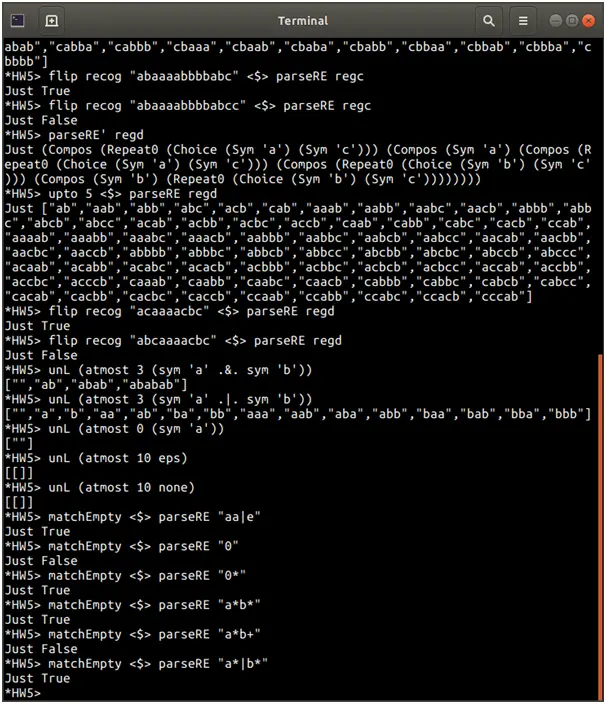
-- D. Strings containing at least one 'a' and at least one 'b', where all 'a's occur earlier than any 'b'.

• Define atmost such that atmost n r means r repeated up to n times. If n is 0 (or negative), atmost n r will be equivalent to eps (that is, repeating r zero times).
• Define matchEmpty, which determines whether the language for a regular expression.

Screenshots of output

Source Code

{-# LANGUAGE TypeFamilies #-} module HW5 where -- Download Lec14.hs and Lec16.hs from Canvas and place them in the same directory as -- HW5.hs import Control.Applicative ((<|>)) import Lec14 (Parser, parse, pSym) import Lec16 pLetter :: Parser Char Char pLetter = pSym 'a' <|> pSym 'b' <|> pSym 'c' parseRE :: (Regular a, Symbol a ~ Char) => String -> Maybe a parseRE = parse (pRE pLetter) parseRE' :: String -> Maybe (RE Char) parseRE' = parseRE -- ***** -- 1. Define string containing regular expressions for the following languages over the -- alphabet {a,b,c}. -- -- Example. Strings containing 'a' two or more times example = "aa+" -- Note that you can use parseRE, recog, and upto to test your expressions. -- -- *HW5> parseRE' example -- Just (Compos (Sym 'a') (Repeat1 (Sym 'a'))) -- *HW5> upto 5 <$> parseRE example -- Just ["aa","aaa","aaaa","aaaaa"] -- *HW5> flip recog "aaa" <$> parseRE example -- Just True -- *HW5> flip recog "aaab" <$> parseRE example -- Just False -- A. The language {"bc","cb","abc","acb"} rega = "(a|e)(bc|cb)" -- B. Strings that begin with 'a' and end with 'b' and do not contain 'c' regb = "a(a|b)*b" -- C. Strings in which 'c' occurs exactly once regc = "(a|b)*c(a|b)*" -- D. Strings containing at least one 'a' and at least one 'b', where all 'a's occur -- earlier than any 'b'. regd = "(a|c)*a(a|c)*(b|c)*b(b|c)*" -- ***** -- 2. Define atmost such that atmost n r means r repeated up to n times. If n is 0 -- (or negative), atmost n r will be equivalent to eps (that is, repeating r zero -- times). -- -- *HW5> unL (atmost 3 (sym 'a' .&. sym 'b')) -- ["","ab","abab","ababab"] -- *HW5> unL (atmost 3 (sym 'a' .|. sym 'b')) -- ["","a","b","aa","ab","ba","bb","aaa","aab","aba","abb","baa","bab","bba","bbb"] -- *HW5> unL (atmost 0 (sym 'a')) -- [""] -- *HW5> unL (atmost 10 eps) -- [[]] -- *HW5> unL (atmost 10 none) -- [[]] atmost :: (Regular a) => Integer -> a -> a atmost n f = if n <= 0 then eps else eps .|. (f .&. atmost (n-1) f) -- ***** -- 3. Define matchEmpty, which determines whether the language for a regular expression -- includes the empty string. -- -- *HW5> matchEmpty <$> parseRE "aa|e" -- Just True -- *HW5> matchEmpty <$> parseRE "0" -- Just False -- *HW5> matchEmpty <$> parseRE "0*" -- Just True -- *HW5> matchEmpty <$> parseRE "a*b*" -- Just True -- *HW5> matchEmpty <$> parseRE "a*b*" -- Just True -- *HW5> matchEmpty <$> parseRE "a*b+" -- Just False matchEmpty :: RE symbol -> Bool matchEmpty (Sym _) = False matchEmpty Empty = True matchEmpty Never = False matchEmpty (Repeat0 _) = True matchEmpty (Repeat1 _) = False matchEmpty (Compos a b) = matchEmpty a && matchEmpty b matchEmpty (Choice a b) = matchEmpty a || matchEmpty b