Create a Program to Implement SVM Classification in Python Assignment Solution

Instructions

Objective

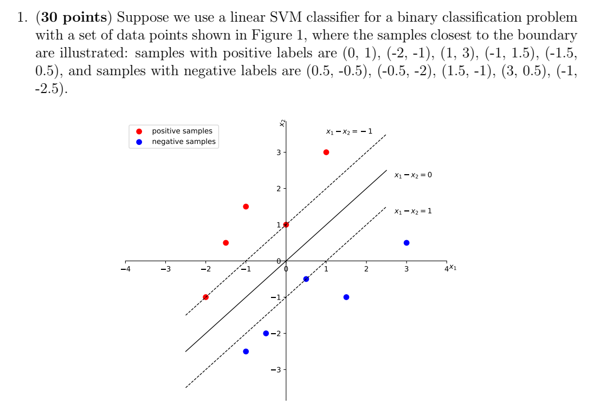
Write a Python homework program to implement SVM classification.

Requirements and Specifications

Source Code

import numpy as np class Tree_node: """ Data structure for nodes in the decision-tree """ def __init__(self,): self.is_leaf = False # whether or not the current node is a leaf node self.feature = None # index of the selected feature (for non-leaf node) self.label = -1 # class label (for leaf node) self.left_child = None # left child node self.right_child = None # right child node class Decision_tree: """ Decision tree with binary features """ def __init__(self,min_entropy): self.min_entropy = min_entropy # min node entropy self.root = None def fit(self,train_x,train_y): # construct the decision-tree with recursion self.root = self.generate_tree(train_x,train_y) def predict(self,test_x): # iterate through all samples prediction = np.zeros([len(test_x),]).astype('int') # placeholder for i in range(len(test_x)): #pass # placeholder node = self.root data = test_x[i,:] while node.left_child or node.right_child: if data[node.feature] == 1: node = node.right_child else: node = node.left_child prediction[i] = node.label return prediction def generate_tree(self,data,label): # initialize the current tree node cur_node = Tree_node() # compute the node entropy node_entropy = self.compute_node_entropy(label) if node_entropy < self.min_entropy: cur_node.isleaf = True mostFrequent = np.argmax(np.bincount(label)) cur_node.label = mostFrequent return cur_node # select the feature that will best split the current non-leaf node selected_feature = self.select_feature(data,label) cur_node.feature = selected_feature # split the data based on the selected feature and start the next level of recursion featureData = data[:,selected_feature] zeros = np.asarray(np.where(featureData == 0))[0] ones = np.asarray(np.where(featureData == 1))[0] leftData = data[zeros] leftLabel = label[zeros] rightData = data[ones] rightLabel = label[ones] cur_node.left_child = self.generate_tree(leftData, leftLabel) cur_node.right_child = self.generate_tree(rightData, rightLabel) return cur_node def select_feature(self,data,label): # iterate through all features and compute their corresponding entropy best_feat = 0 lowestEntropy = float("inf") for i in range(len(data[0])): featureData = data[:,i] zeros = np.asarray(np.where(featureData == 0)) ones = np.asarray(np.where(featureData == 1)) zerosLabels = label[zeros[0]] onesLabels = label[ones[0]] entropy = self.compute_split_entropy(zerosLabels, onesLabels) if entropy < lowestEntropy: lowestEntropy = entropy best_feat = i return best_feat def compute_split_entropy(self,left_y, right_y): # compute the entropy of a potential split, left_y and right_y are labels for the two branches split_entropy = 0 # placeholder leftEntropy = self.compute_node_entropy(left_y) rightEntropy = self.compute_node_entropy(right_y) leftSamples = len(left_y) rightSamples = len(right_y) total = leftSamples + rightSamples split_entropy = leftEntropy * leftSamples/total + rightEntropy * rightSamples/total return split_entropy def compute_node_entropy(self,label): # compute the entropy of a tree node (add 1e-15 inside the log2 when computing the entropy to prevent numerical issue) node_entropy = 0 # placeholder e = 1e-12 totalSamples = len(label) count = np.bincount(label) count = count / totalSamples for j in range(len(count)): node_entropy += -count[j] * np.log2(count[j] + e) return node_entropy