Matlab Program to Implement Range Equations Assignment Solution

% EE 7330 Modern Radar Theory

% Spring 2022 - Project 00

% Team 5

% Trevor Scarberry, Matthew Scharf, Siddhant Sharma

clc

clear all

close all

%% Parameters

%variables

Ptx = 150e3;

Fc = 9.4e9;

tau = 1.2e-6;

PRF = 2e3;

PRI = 1/PRF;

Gtx_dB = 45.25;

Tdw = 18.3e-3;

F0_dB = 2.5;

Ltx_dB = 3.1;

Lrx_dB = 2.4;

Lsp_dB = 3.2;

RT_km = 5:105;

RT = RT_km*1000;

Latm_dB = .16*2*RT_km;

sigma1_dB = 0;

sigma2_dB = -10;

SNRM_dB = 12;

% vT = [150 250 400] * 0.5144447;

vT = [150 250 400];

c = 3e8;

kB = 1.38e-23;

T = 290;

B = 1/tau;

lambda = c/Fc;

Rtgt_km = [25 50 70]; %target ranges, km

Rtgt = Rtgt_km * 1000;

Vtgt = [-15, 5, -10]; %Target velocities, m/s

%convert dB to abs

Gtx = 10^(Gtx_dB/10);

F0 = 10^(F0_dB/10);

Ltx = 10^(Ltx_dB/10);

Lrx = 10^(Lrx_dB/10);

Lsp =10^(Lsp_dB/10);

Latm = 10.^(Latm_dB/10);

SNRM = 10^(SNRM_dB/10);

sigma1 = 10^(sigma1_dB/10);

sigma2 = 10^(sigma2_dB/10);

np = floor(Tdw * PRF);

M = np;

L = Ltx*Lrx*Lsp.*(Latm);

N = kB*B*T*F0;

SNR_M_arr_dB = ones(1,length(RT)) * SNRM_dB; % Need array to plot

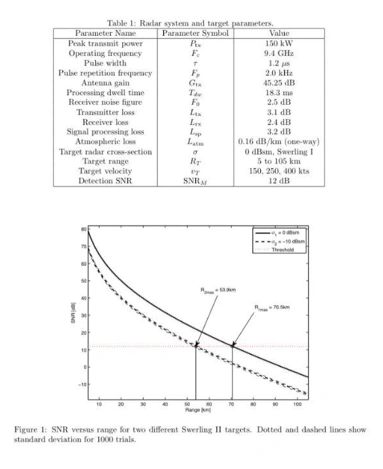
%% 1.a reproduce curves for SNRM versus range

Prx = (Ptx*Gtx^2*lambda^2)./((RT).^4*(4*pi)^3.*L); % here we calculate prc according to equation (2), but without the standard deviations

SNR0 = Prx./N;

% Here we complete the calculations of Prx and SNR for each standard

% deviation (positive and negative)

Prx1 = Prx*sigma1;

SNR1 = M*Prx1/(N);

Prx2 = Prx*sigma2;

SNR2 = M*Prx2/(N);

figure;

plot(RT_km, 10*log10(SNR1), '-b', 'LineWidth', 2);

hold on;

plot(RT_km, 10*log10(SNR2),'-k', 'LineWidth', 2);

hold on;

plot(RT_km, SNR_M_arr_dB,'r--', 'LineWidth', 2);

ylabel('SNR (dB)');

xlabel('Range (km)');

title('SNR vs Range')

legend('\sigma_1 = 0 dBsm ', '\sigma_2 = -10 dBsm','Threshold');

grid on;

xlim([min(RT_km) max(RT_km)]);

%% 1.b monte carlo sim

% we simulate 1000 events of randomness

for n = 1:1000

RCS1 = random('exp',sigma1,[M 1]);

RCS2 = random('exp',sigma2+1,[M 1]);

y1a(n,:) = sum(RCS1)*SNR1/M;

y2a(n,:) = sum(RCS2)*SNR2/M;

end

%obtain mean and standard deviation

y1avg = mean(y1a,1);

y1std = std(y1a,1,1);

y2avg = mean(y2a,1);

y2std = std(y2a,1,1);

%convert to db, create data for plots

y1avg_dB = 10*log10(y1avg);

y1avg_plus_std = 10*log10(y1avg+y1std);

y1avg_minus_std = 10*log10(y1avg-y1std);

y2avg_dB = 10*log10(y2avg);

y2avg_plus_std = 10*log10(y2avg+y2std);

y2avg_minus_std = 10*log10(y2avg-y2std);

%plot

figure;

hold on;

plot(RT_km,y1avg_dB)

plot(RT_km,y1avg_plus_std)

plot(RT_km,y1avg_minus_std)

plot(RT_km, SNR_M_arr_dB,'r--', 'LineWidth', 2);

plot(RT_km,y2avg_dB)

plot(RT_km,y2avg_plus_std)

plot(RT_km,y2avg_minus_std)

xlabel('Range[km]')

ylabel('SNR[dB]')

title('SNR vs Range (n=1000)')

legend('\sigma_1 = 0 dBsm ', '\sigma_2 = -10 dBsm','Threshold');

grid on;

xlim([min(RT_km) max(RT_km)]);

%% Part 2 - Range-Doppler Map

% here we calculate the signal amplitudes according toi equation (17.2) on

% the book

A = sqrt(Prx1);

% The next 3 lines calculates the amplitudes at each of the desired

% locations inside the range of study

A1= sqrt((Ptx*Gtx^2*sigma1*lambda^2)./((Rtgt(1))^4*(4*pi)^3.*L));

A2= sqrt((Ptx*Gtx^2*sigma1*lambda^2)./((Rtgt(2))^4*(4*pi)^3.*L));

A3= sqrt((Ptx*Gtx^2*sigma1*lambda^2)./((Rtgt(3))^4*(4*pi)^3.*L));

% The next line calculates the transmited frequency according to equation

% (17.1) on the book

Fd = 2*Vtgt/lambda;

%resolution = 1/(PRI*M);

% y1 = complex(zeros(length(RT_km),M));

% y2 = complex(zeros(length(RT_km),M));

% y3 = complex(zeros(length(RT_km),M));

%

% for l = 1:length(RT_km)

% for m = 1:M

%

% y1(l,m) = A(l)*exp(-1i*4*pi*Rtgt(1)/lambda)*exp(1i*2*pi*m*PRI*Fd(1));

% y2(l,m) = A(l)*exp(-1i*4*pi*Rtgt(2)/lambda)*exp(1i*2*pi*m*PRI*Fd(2));

% y3(l,m) = A(l)*exp(-1i*4*pi*Rtgt(3)/lambda)*exp(1i*2*pi*m*PRI*Fd(3));

% end

% end

% y0 = y1+y2+y3;

% Y =fftshift(fft(y0,[],2));

% Y1 = fftshift(fft(y1,[],2));

% Y2 = fftshift(fft(y2,[],2));

% Y3 = fftshift(fft(y3,[],2));

% We create the pulse-Doppler data matrix filled with zeros

y1 = complex(zeros(length(RT_km),M));

% Now, for every bin l0 and for every bin on the range M, we calculate

% the spatial Doppler signal

for l = 1:length(Rtgt_km)

for m = 1:M

idx = find(RT_km==Rtgt_km(l)); % One of the problems were here. The variable y1 has the same number

% of rows as elements in the vector

% RT_km, so when the values were

% changed for every value in

% Rtgt_km, the indices used were

% wrong

y1(idx,m) = A1(l)*exp(-1i*4*pi*Rtgt_km(l)/lambda)*exp(1i*2*pi*m*PRI*Fd(l));

end

end

% Now, we apply the fast fourier transform to the matrix and we obtain a

% complex number X + jY

Y1 = fftshift(fft(y1, [], 2), 2); % Another fix was done here. The fftshift and fft

% functions were called with

% incorrect arguments for number of

% dimensions

% Y2 = fftshift(fft(y2,[],2));

% Y3 = fftshift(fft(y3,[],2));

% Here we define the range of frequencies (x) and the space (y)

x = linspace((-PRF/2),(PRF/2),M);

y = linspace(min(RT_km),max(RT_km),length(RT_km));

%

% %plots

% figure

% hold on

% subplot(1,3,1)

% pcolor(x,y,abs((Y1)))

% title('range-doppler plot v = 150')

% xlabel('Doppler Freq (Hz)')

% ylabel('range(km)')

% shading interp

% colormap jet

% colorbar;

% subplot(1,3,2)

% pcolor(x,y,abs((Y2)))

% title('range-doppler plot v = 250')

% xlabel('Doppler Freq (Hz)')

% ylabel('range(km)')

% shading interp

% colormap jet

% colorbar;

% subplot(1,3,3)

% pcolor(x,y,abs((Y3)))

% title('range-doppler plot v = 400')

% xlabel('Doppler Freq (Hz)')

% ylabel('range(km)')

% shading interp

% colormap jet

% colorbar;

figure

hold on

pcolor(x,y,abs(Y1))

title('range-doppler plot')

xlabel('Doppler Freq (Hz)')

ylabel('range(km)')

xlim([-PRF/2,PRF/2]);

ylim([min(RT_km), max(RT_km)]);

shading interp

colormap jet

colorbar;

% figure;

% subplot(3,1,1)

% plot(x,abs(Y1))

% xlabel("Doppler Freq (Hz)");

% ylabel("Range (km)");

% % xlim([min(RT_km), max(RT_km)]);

% grid on;

% subplot(3,1,2)

% plot(x,abs(Y2))

% xlabel("Doppler Freq (Hz)");

% ylabel("Range (km)");

% % xlim([min(RT_km), max(RT_km)]);

% grid on;

% subplot(3,1,3)

% plot(x,abs(Y3))

% xlabel("Doppler Freq (Hz)");

% ylabel("Range (km)");

% % xlim([min(RT_km), max(RT_km)]);

% grid on;