Convert Simple Programming Language into AST Assignment Solution

Instructions

Objective

Write a program to convert a simple programming language into AST.

Requirements and Specifications

Implement to complete an OCAML assignment interpreter for an extended version of the calculator language, again with if and do/check statements. You will write your interpreter in OCaml. We are providing you with a parser generator and driver that builds an explicit parse tree. The provided code also includes the skeleton of a possible solution that converts the parse tree to a syntax tree and then recursively “walks” that tree to affect the interpretation. You are of course welcome to adopt a different skeleton if you prefer. Since this onehas been excised from a complete working solution, however, you may find it a good place to start. The provided code has two main entry points

get_parse_table : grammar -> parse_table = … parse : parse_table -> string -> parse_tree = … The first of these routines returns a parse table, in the format expected as the first argument of the second routine. The second returns a parse tree. (You’ll want to print some of these trees to see what they look like.) If the program has syntax errors (according to the grammar), parse will print an error message (as a side effect) and return a PT_error value (it does not do error recovery). If the input grammar you provide is malformed, you may get unhelpful run-time errors from the parser generator—it isn’t very robust. The grammar takes the form of a list of production sets, each ofwhich is a pair containing the LHS symbol and k right-hand sides, each of which is itself a list of symbols. When get_parse_table builds the parse table, the grammar is augmented with a start production that mentions an explicit end of file $$. Later, parse will remove this production from the resulting parse tree.

Screenshots of output

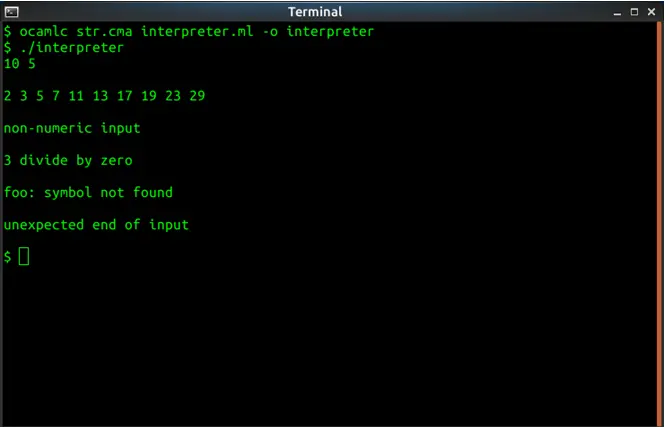
Source Code

(******************************************************************* LL(1) parser generator, syntax tree builder for an extended calculator language, and (skeleton of an) interpreter for the generated syntax trees. If compiled and run, will execute "main()". Alternatively, can be "#use"-ed (or compiled and then "#load"-ed) into the top-level interpreter. *******************************************************************) open List;; (* The List library includes a large collection of useful functions. In the provided code, I've used assoc, exists, filter, find, fold_left, hd, length, map, and rev. *) open Str;; (* for split *) (* The Str library provides a few extra string-processing routines. In particular, it provides "split", which I use to break program input into whitespace-separated words. Note, however, that this library is not automatically available. If you are using the top-level interpreter, you have to say #load "str.cma";; before you say #use "interpreter.ml";; If you are generating an executable from the shell, you have to include the library name on the command line: ocamlc -o interpreter str.cma interpreter.ml *) (* Surprisingly, compose isn't built in. It's included in various widely used commercial packages, but not in the core libraries. *) let compose f g x = f (g x);; type symbol_productions = (string * string list list);; type grammar = symbol_productions list;; type parse_table = (string * (string list * string list) list) list;; (* nt predict_set rhs *) let calc_gram : grammar = [ ("P", [["SL"; "$$"]]) ; ("SL", [["S"; "SL"]; []]) ; ("S", [ ["id"; ":="; "E"]; ["read"; "id"]; ["write"; "E"]]) ; ("E", [["T"; "TT"]]) ; ("T", [["F"; "FT"]]) ; ("TT", [["ao"; "T"; "TT"]; []]) ; ("FT", [["mo"; "F"; "FT"]; []]) ; ("ao", [["+"]; ["-"]]) ; ("mo", [["*"]; ["/"]]) ; ("F", [["id"]; ["num"]; ["("; "E"; ")"]]) ];; let ecg : grammar = [ ("P", [["SL"; "$$"]]) ; ("SL", [["S"; "SL"]; []]) ; ("S", [ ["id"; ":="; "R"]; ["read"; "id"]; ["write"; "R"] ; ["if"; "R"; "SL"; "fi"]; ["do"; "SL"; "od"]; ["check"; "R"] ]) ; ("R", [["E"; "ET"]]) ; ("E", [["T"; "TT"]]) ; ("T", [["F"; "FT"]]) ; ("F", [["id"]; ["num"]; ["("; "R"; ")"]]) ; ("ET", [["ro"; "E"]; []]) ; ("TT", [["ao"; "T"; "TT"]; []]) ; ("FT", [["mo"; "F"; "FT"]; []]) ; ("ro", [["=="]; ["<>"]; ["<"]; [">"]; ["<="]; [">="]]) ; ("ao", [["+"]; ["-"]]) ; ("mo", [["*"]; ["/"]]) ];; (* is e a member of list l? *) let member e l = exists ((=) e) l;; (* OCaml has a built-in quicksort; this was just an exercise. *) let rec sort l = let rec partition pivot l left right = match l with | [] -> (left, right) | c :: rest -> if (compare c pivot) < 0 then partition pivot rest (c :: left) right else partition pivot rest left (c :: right) in match l with | [] -> l | h :: [] -> l | h :: rest -> let (left, right) = partition h rest [] [] in (sort left) @ [h] @ (sort right);; (* leave only one of any consecutive identical elements in list *) let rec unique l = match l with | [] -> l | h :: [] -> l | a :: b :: rest -> if a = b (* structural eq *) then unique (b :: rest) else a :: unique (b :: rest);; let unique_sort l = unique (sort l);; (* Return all individual productions in grammar. *) let productions gram : (string * string list) list = let prods (lhs, rhss) = map (fun rhs -> (lhs, rhs)) rhss in fold_left (@) [] (map prods gram);; (* Return all symbols in grammar. *) let gsymbols gram : string list = unique_sort (fold_left (@) [] (map (compose (fold_left (@) []) snd) gram));; (* Return all elements of l that are not in to_exclude. Assume that both lists are sorted *) let list_minus l to_exclude = let rec helper rest te rtn = match rest with | [] -> rtn | h :: t -> match te with | [] -> (rev rest) @ rtn | h2 :: t2 -> match compare h h2 with | -1 -> helper t te (h :: rtn) | 0 -> helper t t2 rtn | _ -> helper rest t2 rtn in rev (helper l to_exclude []);; (* Return just the nonterminals. *) let nonterminals gram : string list = map fst gram;; (* Return just the terminals. *) let terminals gram : string list = list_minus (gsymbols gram) (unique_sort (nonterminals gram));; (* Return the start symbol. Throw exception if grammar is empty. *) let start_symbol gram : string = fst (hd gram);; let is_nonterminal e gram = member e (nonterminals gram);; let is_terminal e gram = member e (terminals gram);; let union s1 s2 = unique_sort (s1 @ s2);; (* return suffix of lst that begins with first occurrence of sym (or [] if there is no such occurrence) *) let rec suffix sym lst = match lst with | [] -> [] | h :: t -> if h = sym (* structural eq *) then lst else suffix sym t;; (* Return a list of pairs. Each pair consists of a symbol A and a list of symbols beta such that for some alpha, A -> alpha B beta. *) type right_context = (string * string list) list;; let get_right_context (b:string) gram : right_context = fold_left (@) [] (map (fun prod -> let a = fst prod in let rec helper accum rhs = let b_beta = suffix b rhs in match b_beta with | [] -> accum | x :: beta -> (* assert x = b *) helper ((a, beta) :: accum) beta in helper [] (snd prod)) (productions gram));; (* parser generator starts here *) type symbol_knowledge = string * bool * string list * string list;; type knowledge = symbol_knowledge list;; let symbol_field (s, e, fi, fo) = s;; let eps_field (s, e, fi, fo) = e;; let first_field (s, e, fi, fo) = fi;; let follow_field (s, e, fi, fo) = fo;; let initial_knowledge gram : knowledge = map (fun a -> (a, false, [], [])) (nonterminals gram);; let get_symbol_knowledge (a:string) (kdg:knowledge) : symbol_knowledge = find (fun (s, e, fi, fo) -> s = a) kdg;; (* Can word list w generate epsilon based on current estimates? if w is an empty list, yes if w is a single terminal, no if w is a single nonterminal, look it up if w is a non-empty list, "iterate" over elements *) let rec generates_epsilon (w:string list) (kdg:knowledge) gram : bool = match w with | [] -> true | h :: t -> if is_terminal h gram then false else eps_field (get_symbol_knowledge h kdg) && generates_epsilon t kdg gram;; (* Return FIRST(w), based on current estimates. if w is an empty list, return [] [empty set] if w is a single terminal, return [w] if w is a single nonterminal, look it up if w is a non-empty list, "iterate" over elements *) let rec first (w:string list) (kdg:knowledge) gram : (string list) = match w with | [] -> [] | x :: _ when is_terminal x gram -> [x] | x :: rest -> let s = first_field (get_symbol_knowledge x kdg) in if generates_epsilon [x] kdg gram then union s (first rest kdg gram) else s;; let follow (a:string) (kdg:knowledge) : string list = follow_field (get_symbol_knowledge a kdg);; let rec map3 f l1 l2 l3 = match (l1, l2, l3) with | ([], [], []) -> [] | (h1 :: t1, h2 :: t2, h3 :: t3) -> (f h1 h2 h3) :: map3 f t1 t2 t3 | _ -> raise (Failure "mismatched_lists");; (* Return knowledge structure for grammar. Start with (initial_knowledge grammar) and "iterate", until the structure doesn't change. Uses (get_right_context B gram), for all nonterminals B, to help compute follow sets. *) let get_knowledge gram : knowledge = let nts : string list = nonterminals gram in let right_contexts : right_context list = map (fun s -> get_right_context s gram) nts in let rec helper kdg = let update : symbol_knowledge -> symbol_productions -> right_context -> symbol_knowledge = fun old_sym_kdg sym_prods sym_right_context -> let my_first s = first s kdg gram in let my_eps s = generates_epsilon s kdg gram in let filtered_follow p = if my_eps (snd p) then (follow (fst p) kdg) else [] in ( symbol_field old_sym_kdg, (* nonterminal itself *) (eps_field old_sym_kdg) (* previous estimate *) || (fold_left (||) false (map my_eps (snd sym_prods))), union (first_field old_sym_kdg) (* previous estimate *) (fold_left union [] (map my_first (snd sym_prods))), union (union (follow_field old_sym_kdg) (* previous estimate *) (fold_left union [] (map my_first (map (fun p -> match snd p with | [] -> [] | h :: t -> [h]) sym_right_context)))) (fold_left union [] (map filtered_follow sym_right_context)) ) in (* end of update *) let new_kdg = map3 update kdg gram right_contexts in (* body of helper: *) if new_kdg = kdg then kdg else helper new_kdg in (* body of get_knowledge: *) helper (initial_knowledge gram);; let get_parse_table (gram:grammar) : parse_table = let kdg = get_knowledge gram in map (fun (lhs, rhss) -> (lhs, (map (fun rhs -> (union (first rhs kdg gram) (if (generates_epsilon rhs kdg gram) then (follow lhs kdg) else []), rhs)) rhss))) gram;; (* convert string to list of char *) let explode (s:string) : char list = let rec exp i l = if i < 0 then l else exp (i-1) (s.[i] :: l) in exp (String.length s - 1) [];; (* convert list of char to string (This uses imperative features. It used to be a built-in.) *) let implode (l:char list) : string = let res = Bytes.create (length l) in let rec imp i l = match l with | [] -> Bytes.to_string res | c :: l -> Bytes.set res i c; imp (i + 1) l in imp 0 l;; (******************************************************************* Scanner. Note that for the sake of generality (so you can experiment with other languages), this accepts certain tokens that are not needed in the calculator language. *******************************************************************) type token = string * string;; (* category * name *) let tokenize (program:string) : token list = let get_id prog = let rec gi tok p = match p with | c :: rest when (('a' <= c && c <= 'z') || ('A' <= c && c <= 'Z') || ('0' <= c && c <= '9') || (c = '_')) -> gi (c :: tok) rest | _ -> (implode (rev tok), p) in gi [] prog in let get_int prog = let rec gi tok p = match p with | c :: rest when ('0' <= c && c <= '9') -> gi (c :: tok) rest | _ -> (implode (rev tok), p) in gi [] prog in let get_num prog = let (tok, rest) = get_int prog in match rest with | '.' :: c :: r when ('0' <= c && c <= '9') -> let (tok2, rest2) = get_int (c :: r) in ((tok ^ "." ^ tok2), rest2) | _ -> (tok, rest) in let rec get_error tok prog = match prog with | [] -> (implode (rev tok), prog) | c :: rest -> match c with | ':' | '+' | '-' | '*' | '/' | '(' | ')' | '[' | ']' | '_' | '<' | '>' | '=' | '!' | ',' | 'a'..'z' | 'A'..'Z' | '0'..'9' -> (implode (rev tok), prog) | _ -> get_error (c :: tok) rest in let rec skip_space prog = match prog with | [] -> [] | c :: rest -> if (c = ' ' || c = '\n' || c = '\r' || c = '\t') then skip_space rest else prog in let rec tkize toks prog = match prog with | [] -> (("$$" :: toks), []) | '\n' :: rest | '\r' :: rest | '\t' :: rest | ' ' :: rest -> tkize toks (skip_space prog) | ':' :: '=' :: rest -> tkize (":=" :: toks) rest | ':' :: rest -> tkize (":" :: toks) rest | '+' :: rest -> tkize ("+" :: toks) rest | '-' :: rest -> tkize ("-" :: toks) rest | '*' :: rest -> tkize ("*" :: toks) rest | '/' :: rest -> tkize ("/" :: toks) rest | '(' :: rest -> tkize ("(" :: toks) rest | ')' :: rest -> tkize (")" :: toks) rest | '[' :: rest -> tkize ("[" :: toks) rest | ']' :: rest -> tkize ("]" :: toks) rest | '<' :: '>' :: rest -> tkize ("<>" :: toks) rest | '<' :: '=' :: rest -> tkize ("<=" :: toks) rest | '<' :: rest -> tkize ("<" :: toks) rest | '>' :: '=' :: rest -> tkize (">=" :: toks) rest | '>' :: rest -> tkize (">" :: toks) rest | '=' :: '=' :: rest -> tkize ("==" :: toks) rest | ',' :: rest -> tkize ("," :: toks) rest | h :: t -> match h with | '0'..'9' -> let (t, rest) = get_num prog in tkize (t :: toks) rest | 'a'..'z' | 'A'..'Z' | '_' -> let (t, rest) = get_id prog in tkize (t :: toks) rest | c -> let (t, rest) = get_error [c] t in tkize (t :: toks) rest in let (toks, _) = (tkize [] (explode program)) in let categorize tok = match tok with | "array" | "begin" | "check" | "do" | "else" | "end" | "fi" | "float" | "for" | "if" | "int" | "od" | "proc" | "read" | "real" | "repeat" | "trunc" | "while" | "write" | ":=" | ":" | "+" | "-" | "*" | "/" | "(" | ")" | "[" | "]" | "<" | "<=" | ">" | ">=" | "==" | "<>" | "," | "$$" -> (tok, tok) | _ -> match tok.[0] with | '0'..'9' -> ("num", tok) | 'a'..'z' | 'A'..'Z' | '_' -> ("id", tok) | _ -> ("error", tok) in map categorize (rev toks);; (******************************************************************* The main parse routine below returns a parse tree (or PT_error if the input program is syntactically invalid). To build that tree it employs a simplified version of the "attribute stack" described in Section 4.5.2 (pages 50-55) on the PLP companion site. When it predicts A -> B C D, the parser pops A from the parse stack and then, before pushing D, C, and B (in that order), it pushes a number (in this case 3) indicating the length of the right hand side. It also pushes A into the attribute stack. When it matches a token, the parser pushes this into the attribute stack as well. Finally, when it encounters a number (say k) in the stack (as opposed to a character string), the parser pops k+1 symbols from the attribute stack, joins them together into a list, and pushes the list back into the attribute stack. These rules suffice to accumulate a complete parse tree into the attribute stack at the end of the parse. Note that everything is done functionally. We don't really modify the stacks; we pass new versions to a tail recursive routine. *******************************************************************) (* Extract grammar from parse-tab, so we can invoke the various routines that expect a grammar as argument. *) let grammar_of (parse_tab:parse_table) : grammar = map (fun p -> (fst p, (fold_left (@) [] (map (fun (a, b) -> [b]) (snd p))))) parse_tab;; type parse_tree = (* among other things, parse_trees are *) | PT_error (* the elements of the attribute stack *) | PT_id of string | PT_num of string | PT_term of string | PT_nt of (string * parse_tree list);; (* Pop rhs-len + 1 symbols off the attribute stack, assemble into a production, and push back onto the stack. *) let reduce_1_prod (astack:parse_tree list) (rhs_len:int) : parse_tree list = let rec helper atk k prod = match (k, atk) with | (0, PT_nt(nt, []) :: t) -> PT_nt(nt, prod) :: t | (n, h :: t) when n <> 0 -> helper t (k - 1) (h :: prod) | _ -> raise (Failure "expected nonterminal at top of astack") in helper astack rhs_len [];; let sum_ave_prog = "read a read b sum := a + b write sum write sum / 2";; let primes_prog = " read n cp := 2 do check n > 0 found := 0 cf1 := 2 cf1s := cf1 * cf1 do check cf1s <= cp cf2 := 2 pr := cf1 * cf2 do check pr <= cp if pr == cp found := 1 fi cf2 := cf2 + 1 pr := cf1 * cf2 od cf1 := cf1 + 1 cf1s := cf1 * cf1 od if found == 0 write cp n := n - 1 fi cp := cp + 1 od";; type parse_action = PA_error | PA_prediction of string list;; (* Double-index to find prediction (list of RHS symbols) for nonterminal nt and terminal t. Return PA_error if not found. *) let get_parse_action (nt:string) (t:string) (parse_tab:parse_table) : parse_action = let rec helper l = match l with | [] -> PA_error | (fs, rhs) :: rest -> if member t fs then PA_prediction(rhs) else helper rest in helper (assoc nt parse_tab);; type ps_item = | PS_end of int | PS_sym of string;; (* Parse program according to grammar. [Commented-out code would print predictions and matches (imperatively) along the way.] Return parse tree if the program is in the language; PT_error if it's not. *) let parse (parse_tab:parse_table) (program:string) : parse_tree = let die msg = begin print_string ("syntax error: " ^ msg); print_newline (); PT_error end in let gram = grammar_of parse_tab in let rec helper pstack tokens astack = match pstack with | [] -> if tokens = [] then (* assert: astack is nonempty *) hd astack else die "extra input beyond end of program" | PS_end(n) :: ps_tail -> helper ps_tail tokens (reduce_1_prod astack n) | PS_sym(tos) :: ps_tail -> match tokens with | [] -> die "unexpected end of program" | (term, tok) :: more_tokens -> (* if tok is an individual identifier or number, term will be a generic "id" or "num" *) if is_terminal tos gram then if tos = term then begin (* print_string (" match " ^ tos); print_string (if tos <> term (* value comparison *) then (" (" ^ tok ^ ")") else ""); print_newline (); *) helper ps_tail more_tokens (( match term with | "id" -> PT_id tok | "num" -> PT_num tok | _ -> PT_term tok ) :: astack) end (* note push of tok into astack *) else die ("expected " ^ tos ^ " ; saw " ^ tok) else (* nonterminal *) match get_parse_action tos term parse_tab with | PA_error -> die ("no prediction for " ^ tos ^ " when seeing " ^ tok) | PA_prediction(rhs) -> begin (* print_string (" predict " ^ tos ^ " ->"); print_string (fold_left (fun a b -> a ^ " " ^ b) "" rhs); print_newline (); *) helper ((fold_left (@) [] (map (fun s -> [PS_sym(s)]) rhs)) @ [PS_end(length rhs)] @ ps_tail) tokens (PT_nt(tos, []) :: astack) end in helper [PS_sym(start_symbol gram)] (tokenize program) [];; let cg_parse_table = get_parse_table calc_gram;; let ecg_parse_table = get_parse_table ecg;; (******************************************************************* Everything above this point in the file is complete and (I think) usable as-is. The rest of the file, from here down, is a skeleton for the extra code you need to write. It has been excised from my working solution to the assignment. You are welcome, of course, to use a different organization if you prefer. This is provided in the hope you may find it useful. *******************************************************************) type ast_sl = ast_s list and ast_s = | AST_error | AST_assign of (string * ast_e) | AST_read of string | AST_write of ast_e | AST_if of (ast_e * ast_sl) | AST_do of ast_sl | AST_check of ast_e and ast_e = | AST_binop of (string * ast_e * ast_e) | AST_id of string | AST_num of string;; let rec ast_ize_prog (p:parse_tree) : ast_sl = match p with | PT_nt ("P", [pt_stl; PT_term "$$"]) -> (* match program and end *) ast_ize_stmt_list pt_stl (* go to statement list *) | _ -> raise (Failure "malformed parse tree in ast_ize_prog") and ast_ize_stmt_list (sl:parse_tree) : ast_sl = match sl with | PT_nt ("SL", []) -> [] (* match empty list *) | PT_nt ("SL", [pt_st; pt_stl]) -> (* match statement and rest *) (* process statement and recurse with rest of list *) (ast_ize_stmt pt_st) :: (ast_ize_stmt_list pt_stl) | _ -> raise (Failure "malformed parse tree in ast_ize_stmt_list") and ast_ize_stmt (s:parse_tree) : ast_s = match s with | PT_nt ("S", [PT_id lhs; PT_term ":="; expr]) -> (* if assignment, get id and expression and return assign node *) AST_assign (lhs, (ast_ize_expr expr)) | PT_nt ("S", [PT_term "read"; PT_id id]) -> (* if read, get id and return read node *) AST_read id | PT_nt ("S", [PT_term "write"; expr]) -> (* if write, get expression and return write node *) AST_write (ast_ize_expr expr) | PT_nt ("S", [PT_term "if"; expr; pt_stl; PT_term "fi"]) -> (* when if, get expression, process statement list and return if node *) AST_if (ast_ize_expr expr, ast_ize_stmt_list pt_stl) | PT_nt ("S", [PT_term "do"; pt_stl; PT_term "od"]) -> (* if do, process statement list and return do node *) AST_do (ast_ize_stmt_list pt_stl) | PT_nt ("S", [PT_term "check"; expr]) -> (* if check, get expression and return check node *) AST_check (ast_ize_expr expr) | _ -> raise (Failure "malformed parse tree in ast_ize_stmt") and ast_ize_expr (e:parse_tree) : ast_e = (* e is an R, E, T, or F parse tree node *) match e with | PT_nt ("R", [expr; pt_et]) -> (* match R node *) (* if R node, recurse expression and return reln tail *) ast_ize_reln_tail (ast_ize_expr expr) pt_et | PT_nt ("E", [expr; pt_et]) -> (* match E node *) (* if E node, recurse expression and return expr tail *) ast_ize_expr_tail (ast_ize_expr expr) pt_et | PT_nt ("T", [expr; pt_et]) -> (* match T node *) (* if T node, recurse expression and return expr tail *) ast_ize_expr_tail (ast_ize_expr expr) pt_et | PT_nt ("F", [PT_id id]) -> (* match F id node *) (* get id and return id node *) AST_id id | PT_nt ("F", [PT_num num]) -> (* match F num node *) (* get num and return num node *) AST_num num (* match F parenthesis node *) | PT_nt ("F", [PT_term "("; expr; PT_term ")"]) -> (* recurse expression, return result *) ast_ize_expr expr | _ -> raise (Failure "malformed parse tree in ast_ize_expr") and ast_ize_reln_tail (lhs:ast_e) (tail:parse_tree) : ast_e = (* lhs in an inherited attribute. tail is an ET parse tree node *) match tail with | PT_nt ("ET", []) -> (* match empty ET node *) lhs (* simply return expression *) | PT_nt ("ET", [PT_nt ("ro", [PT_term op]); pt_et]) -> (* match ET op node *) (* build binomial operation with lhs expression and rest of expression*) AST_binop (op, lhs, ast_ize_expr pt_et) | _ -> raise (Failure "malformed parse tree in ast_ize_reln_tail") and ast_ize_expr_tail (lhs:ast_e) (tail:parse_tree) : ast_e = (* lhs in an inherited attribute. tail is a TT or FT parse tree node *) match tail with | PT_nt ("TT", []) -> (* match empty TT node *) lhs (* simply return expression *) (* match TT op node *) | PT_nt ("TT", [PT_nt ("ao", [PT_term op]); pt_et; pt_tt]) -> (* build binomial operation with expression and rest of expression and recurse using built binop *) ast_ize_expr_tail (AST_binop (op, lhs, ast_ize_expr pt_et)) pt_tt | PT_nt ("FT", []) -> (* match empty FT node *) lhs (* simply return expression *) (* match FT op node *) | PT_nt ("FT", [PT_nt ("mo", [PT_term op]); pt_et; pt_tt]) -> (* build binomial operation with lhs expression and rest of expression and recurse using built binop *) ast_ize_expr_tail (AST_binop (op, lhs, ast_ize_expr pt_et)) pt_tt | _ -> raise (Failure "malformed parse tree in ast_ize_expr_tail") ;; (******************************************************************* Interpreter *******************************************************************) type memory = (string * int) list;; (* name * val *) (* If you do the extra credit, you might want an extra Boolean field in the tuple to indicate whether the value has been used. *) type value = (* an integer or an error message *) | Value of int | Error of string;; (* concatenate strings, with a separator in between if both were nonempty *) let str_cat sep a b = match (a, b) with | (a, "") -> a | ("", b) -> b | (_, _) -> a ^ sep ^ b;; type status = | Good | Bad (* run-time error *) | Done;; (* failed check *) (* Input to a calculator program is just a sequence of numbers. We use the standard Str library to split the single input string into whitespace-separated words, each of which is subsequently checked for valid integer format. *) let rec interpret (ast:ast_sl) (full_input:string) : string = let inp = split (regexp "[ \t\n\r]+") full_input in let (_, _, _, outp) = interpret_sl ast [] inp [] in (fold_left (str_cat " ") "" outp) ^ "\n" and interpret_sl (sl:ast_sl) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = (* ok? new_mem new_input new_output *) match sl with | [] -> (Good, mem, inp, outp) (* if end of statements, return *) | st::sts -> match (interpret_s st mem inp outp) with (* recurse to next statement *) | (Good, m, i, o) -> interpret_sl sts m i o (* if done or bad, return value unchanged *) | r -> r (* NB: the following routine is complete. You can call it on any statement node and it figures out what more specific case to invoke. *) and interpret_s (s:ast_s) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = match s with | AST_assign(id, expr) -> interpret_assign id expr mem inp outp | AST_read(id) -> interpret_read id mem inp outp | AST_write(expr) -> interpret_write expr mem inp outp | AST_if(cond, sl) -> interpret_if cond sl mem inp outp | AST_do(sl) -> interpret_do sl mem inp outp | AST_check(cond) -> interpret_check cond mem inp outp | AST_error -> raise (Failure "cannot interpret erroneous tree") and interpret_assign (lhs:string) (rhs:ast_e) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = (* evaluate expression and match result *) match (interpret_expr rhs mem) with | (Value v, new_mem) (* remove old variable and use new value *) -> (Good, (lhs, v) :: remove_assoc lhs new_mem, inp, outp) | (Error es, new_mem) -> (Bad, new_mem, inp, outp @ [es]) (* return error string as output *) and interpret_read (id:string) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = match inp with (* if no more input values it's an error *) | [] -> (Bad, mem, inp, outp @ ["unexpected end of input"]) | v::inps -> if string_match (regexp "[0-9]+$") v 0 then (* if a valid number *) (* remove old variable, convert input to integer and add new var *) (Good, (id, int_of_string v) :: remove_assoc id mem, inps, outp) else (Bad, mem, inp, outp @ ["non-numeric input"]) and interpret_write (expr:ast_e) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = (* evaluate expression and match result *) match (interpret_expr expr mem) with (* add expression value to output *) | (Value v, new_mem) -> (Good, new_mem, inp, outp @ [string_of_int v]) (* return error string as output *) | (Error es, new_mem) -> (Bad, new_mem, inp, outp @ [es]) and interpret_if (cond:ast_e) (sl:ast_sl) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = (* evaluate expression and match result *) match (interpret_expr cond mem) with | (Value 0, new_mem) -> (Good, new_mem, inp, outp) (* if false, return *) (* if true, interpret the statements inside the if *) | (Value _, new_mem) -> interpret_sl sl new_mem inp outp (* return error string as output *) | (Error es, new_mem) -> (Bad, new_mem, inp, outp @ [es]) and interpret_do (sl:ast_sl) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = (* interpret statements in do *) match interpret_sl sl mem inp outp with (* if loop is done, return last state *) | (Done, m, i, o) -> (Good, m, i, o) (* if good, recurse using last state *) | (Good, m, i, o) -> interpret_do sl m i o (* if bad, simply return it *) | b -> b and interpret_check (cond:ast_e) (mem:memory) (inp:string list) (outp:string list) : status * memory * string list * string list = (* evaluate condition and match result *) match (interpret_expr cond mem) with | (Value 0, new_mem) -> (Done, new_mem, inp, outp) (* if false, we are done*) | (Value _, new_mem) -> (Good, new_mem, inp, outp) (* if true, continue *) (* return error string as output *) | (Error es, new_mem) -> (Bad, new_mem, inp, outp @ [es]) and interpret_expr (expr:ast_e) (mem:memory) : value * memory = match expr with (* for an id, return its value *) | AST_id id -> (* if variable exists return its value and var list *) if mem_assoc id mem then (Value (assoc id mem), mem) (* else return error *) else (Error (id ^ ": symbol not found"), mem) (* for a number, return its value *) | AST_num num -> (Value (int_of_string num), mem) | AST_binop (op, expr1, expr2) -> match interpret_expr expr1 mem with | (Error e1, m1) -> (Error e1, m1) | (Value v1, m1) -> match interpret_expr expr2 m1 with | (Error e2, m2) -> (Error e2, m2) | (Value v2, m2) -> (* make operation and return result, relational operators return values 0 or 1 to indicate false or true, respectively *) match op with | "==" -> if v1 == v2 then (Value 1, m2) else (Value 0, m2) | "<>" -> if v1 <> v2 then (Value 1, m2) else (Value 0, m2) | "<" -> if v1 < v2 then (Value 1, m2) else (Value 0, m2) | ">" -> if v1 > v2 then (Value 1, m2) else (Value 0, m2) | "<=" -> if v1 <= v2 then (Value 1, m2) else (Value 0, m2) | ">=" -> if v1 >= v2 then (Value 1, m2) else (Value 0, m2) | "+" -> (Value (v1 + v2), m2) | "-" -> (Value (v1 - v2), m2) | "*" -> (Value (v1 * v2), m2) | "/" -> if v2 <> 0 then (Value (v1 / v2), m2) else (Error "divide by zero", m2) (* last one shouldn't happen, added to avoid warnings *) | x -> (Error ("unknown operator " ^ x), m2) (******************************************************************* Testing *******************************************************************) let sum_ave_parse_tree = parse ecg_parse_table sum_ave_prog;; let sum_ave_syntax_tree = ast_ize_prog sum_ave_parse_tree;; let primes_parse_tree = parse ecg_parse_table primes_prog;; let primes_syntax_tree = ast_ize_prog primes_parse_tree;; let ecg_run prog inp = interpret (ast_ize_prog (parse ecg_parse_table prog)) inp;; let main () = print_string (interpret sum_ave_syntax_tree "4 6"); (* should print "10 5" *) print_newline (); print_string (interpret primes_syntax_tree "10"); (* should print "2 3 5 7 11 13 17 19 23 29" *) print_newline (); print_string (interpret sum_ave_syntax_tree "4 foo"); (* should print "non-numeric input" *) print_newline (); print_string (ecg_run "write 3 write 2 / 0" ""); (* should print "3 divide by zero" *) print_newline (); print_string (ecg_run "write foo" ""); (* should print "foo: symbol not found" *) print_newline (); print_string (ecg_run "read a read b" "3"); (* should print "unexpected end of input" *) print_newline ();; (* Execute function "main" iff run as a stand-alone program. *) if !Sys.interactive then () else main ();;