Write Theorems Using AGDA To Prove 7 Lemmas Haskell Assignment Solutions

Instructions

Objective

Write a program using AGDA to prove 7 lemmas in Haskell.

Requirements and Specifications

• Reading

  Read Chapters 2, 3, and 4 of Verified Functional Programming in Agda, available for free (on campus or VPN) here:

• Installing Agda

  Agda is installed on the CS Windows computers. To remote in, see https://clas.uiowa.edu/linux/services/vmwareview. But you will probably find it worth the effort to install Agda on your own computer. For Windows, the easiest thing is to use our installer:

  https://homepage.divms.uiowa.edu/~astump/agda/Agda2.6.0.1.v1.msi Otherwise, try following the directions on the Agda wiki, here: https://wiki.portal.chalmers.se/agda/pmwiki.php. Essentially, you first do cabal install Agda and then agda-mode setup (the latter probably requires that you add ~/.cabal/bin to your path).

  Open up bool.agda in the IAL. You should see (Agda) at the bottom, but probably will get some error message from emacs. This is because emacs cannot find the "agda" program. We can tell emacs where that program is as follows. Type "Alt-x" and then "customize-group" (no quotes). Hit enter. Then type "agda2" (again no quotes) and hit enter. You will see a list of options. Near the bottom is one for "Agda Program Name". You want to change this one. You click on the little triangle, and you should see a text box that will say "agda". You want to change that to the full path for the agda program on your computer. You figure out what that path is by opening a terminal and typing "which agda" (no quotes), then enter. Copy that path to the little text box (replacing "agda"). Then click the button right under that line that says "State" and select "Save for future sessions". Close emacs and open it up again. If everything goes well, now typing Control-c Control-l in bool.agda should work with syntax highlighting.

• Installing the IAL

  You clone the repo here from GitHub:

  https://github.com/cedille/ial

• Configuring and testing Agda and the IAL [10 points]

  Finally, you need to tell Agda how to find the Iowa Agda Library. If you are using a CS Windows machine, then open the file h:/.emacs. Otherwise, open ~/.emacs in emacs (you type "Control-x Control-f ~/.emacs"). Add the following text, where instead of the word PATH, you should have the path to your copy of the IAL (wherever you put it):

  (custom-set-variables '(agda2-program-args (quote ("--include-path=PATH"))))

  That should be a single forward tick mark on the second line of that code (might render incorrectly in this PDF). On Windows, I found I could put backslashes if I escaped them (double backslash), like this (where Myself is, of course, your actual Windows username):

  C:\\Users\\Myself\\Documents\\ial. To prove that all this is working for you, open bool.agda in the IAL and type Control-c Control-l to load the file with Agda. If this succeeds you should get syntax highlighting for the file. Now take a screenshot called ial-screenshot.png, capturing your Emacs window with bool.agda highlighted. (I found that for some reason, Agda often says "Another command is currently in progress" when I do this, and I must first type Control-c Control-x Control-r to restart Agda, and then do Control-c Control-l.)

Screenshots of output

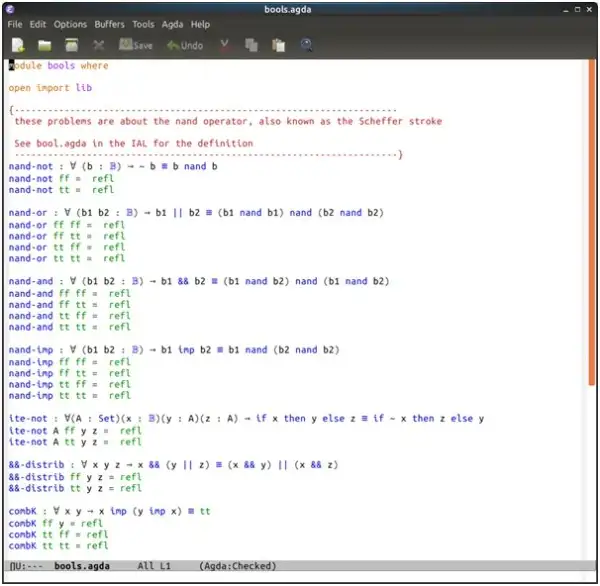
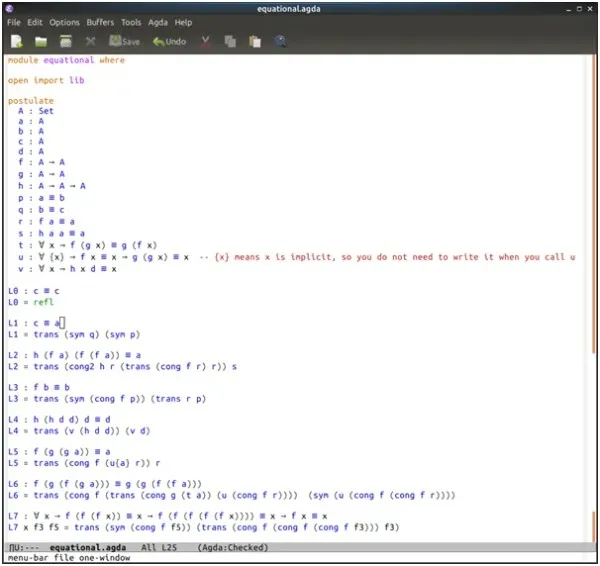
Source Code

Bools.agda

module bools where open import lib {--------------------------------------------------------------------- these problems are about the nand operator, also known as the Scheffer stroke See bool.agda in the IAL for the definition ---------------------------------------------------------------------} nand-not : ∀ (b : 𝔹) → ~ b ≡ b nand b nand-not ff = refl nand-not tt = refl nand-or : ∀ (b1 b2 : 𝔹) → b1 || b2 ≡ (b1 nand b1) nand (b2 nand b2) nand-or ff ff = refl nand-or ff tt = refl nand-or tt ff = refl nand-or tt tt = refl nand-and : ∀ (b1 b2 : 𝔹) → b1 && b2 ≡ (b1 nand b2) nand (b1 nand b2) nand-and ff ff = refl nand-and ff tt = refl nand-and tt ff = refl nand-and tt tt = refl nand-imp : ∀ (b1 b2 : 𝔹) → b1 imp b2 ≡ b1 nand (b2 nand b2) nand-imp ff ff = refl nand-imp ff tt = refl nand-imp tt ff = refl nand-imp tt tt = refl ite-not : ∀(A : Set)(x : 𝔹)(y : A)(z : A) → if x then y else z ≡ if ~ x then z else y ite-not A ff y z = refl ite-not A tt y z = refl &&-distrib : ∀ x y z → x && (y || z) ≡ (x && y) || (x && z) &&-distrib ff y z = refl &&-distrib tt y z = refl combK : ∀ x y → x imp (y imp x) ≡ tt combK ff y = refl combK tt ff = refl combK tt tt = refl

Equational.agda

module equational where open import lib postulate A : Set a : A b : A c : A d : A f : A → A g : A → A h : A → A → A p : a ≡ b q : b ≡ c r : f a ≡ a s : h a a ≡ a t : ∀ x → f (g x) ≡ g (f x) u : ∀ {x} → f x ≡ x → g (g x) ≡ x -- {x} means x is implicit, so you do not need to write it when you call u v : ∀ x → h x d ≡ x L0 : c ≡ c L0 = refl L1 : c ≡ a L1 = trans (sym q) (sym p) L2 : h (f a) (f (f a)) ≡ a L2 = trans (cong2 h r (trans (cong f r) r)) s L3 : f b ≡ b L3 = trans (sym (cong f p)) (trans r p) L4 : h (h d d) d ≡ d L4 = trans (v (h d d)) (v d) L5 : f (g (g a)) ≡ a L5 = trans (cong f (u{a} r)) r L6 : f (g (f (g a))) ≡ g (g (f (f a))) L6 = trans (cong f (trans (cong g (t a)) (u (cong f r)))) (sym (u (cong f (cong f r)))) L7 : ∀ x → f (f (f x)) ≡ x → f (f (f (f (f x)))) ≡ x → f x ≡ x L7 x f3 f5 = trans (sym (cong f f5)) (trans (cong f (cong f (cong f f3))) f3)