Implement Parser and Interpreter for Simple Programming Language In OCAML Assignment Solution
July 02, 2024
-(1).png){kind=avatar}
Dr. Kristen
🇦🇺 Australia
OCaml
Dr. Kristen R. West holds a PhD in Computer Science from the University of Melbourne, Australia. With 9 years of experience, she has completed over 700 OCaml assignments. Dr. West's expertise spans across data structures, compiler design, and functional programming languages, providing students with expert guidance and support to excel in their OCaml coursework.
Key Topics
- Instructions
- Requirements and Specifications
Tip of the day
News
Instructions
Objective
Write a program in OCAML to implement Parser and interpreter for simple programming language in OCAML.
Requirements and Specifications
Implement a series of extensions to the interpreter for the language called PROC that we saw in class. The concrete syntax of the extensions, the abstract syntax of the extensions (ast.ml) and the parser that converts the concrete syntax into the abstract syntax is already provided for you. Your task is to complete the OCAML assignment definition of the interpreter, that is, the function eval_expr so that it is capable of handling the new language features.
Before addressing the extensions, we briefly recall the concrete and abstract syntax of PROC. The concrete syntax is given by the grammar in Fig. 1. Each line in this grammar is called a production of the grammar. We will be adding new productions to this grammar corresponding to the extensions of PROC that we shall study. These shall be presented in
Section 3.
Next we recall the abstract syntax of PROC, as presented in class. We shall also be extending this syntax with new cases for the new language features that we shall add to PROC.
Screenshots of output
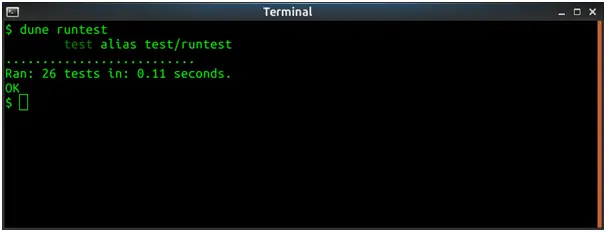
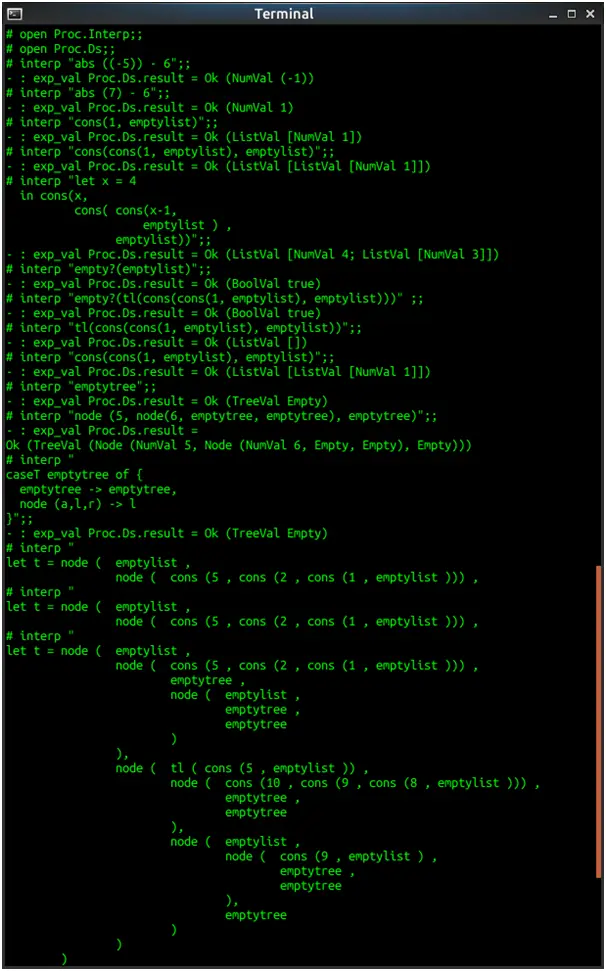
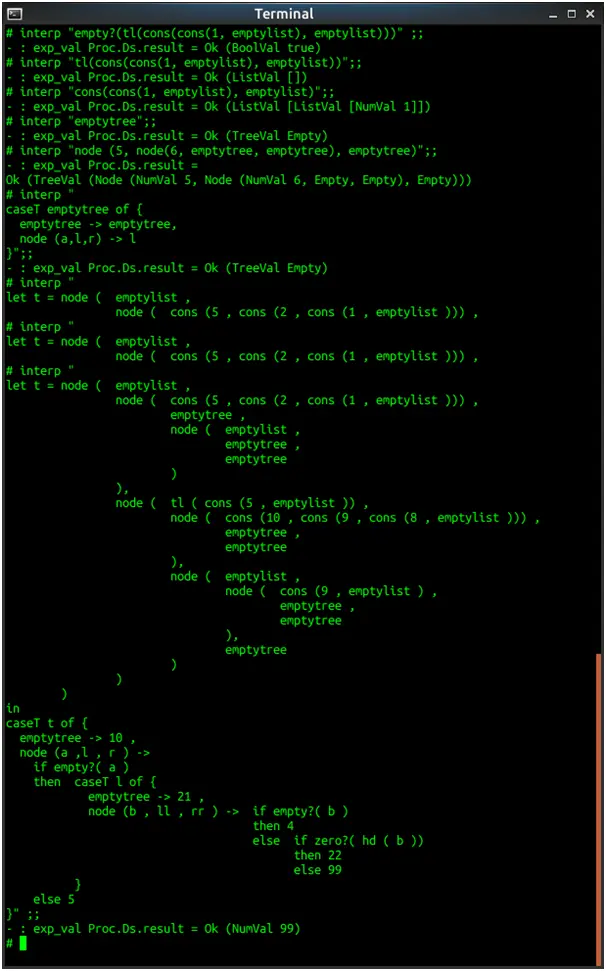
Source Code
open Ast
open Ds
let rec apply_proc : exp_val -> exp_val -> exp_val ea_result =
fun f a ->
match f with
| ProcVal (id,body,env) ->
return env >>+
extend_env id a >>+
eval_expr body
| _ -> error "apply_proc: Not a procVal"
and
eval_expr : expr -> exp_val ea_result = fun e ->
match e with
| Int(n) ->
return @@ NumVal n
| Var(id) ->
apply_env id
| Add(e1,e2) ->
eval_expr e1 >>=
int_of_numVal >>= fun n1 ->
eval_expr e2 >>=
int_of_numVal >>= fun n2 ->
return @@ NumVal (n1+n2)
| Sub(e1,e2) ->
eval_expr e1 >>=
int_of_numVal >>= fun n1 ->
eval_expr e2 >>=
int_of_numVal >>= fun n2 ->
return @@ NumVal (n1-n2)
| Mul(e1,e2) ->
eval_expr e1 >>=
int_of_numVal >>= fun n1 ->
eval_expr e2 >>=
int_of_numVal >>= fun n2 ->
return @@ NumVal (n1*n2)
| Div(e1,e2) ->
eval_expr e1 >>=
int_of_numVal >>= fun n1 ->
eval_expr e2 >>=
int_of_numVal >>= fun n2 ->
if n2==0
then error "Division by zero"
else return @@ NumVal (n1/n2)
| Let(id,def,body) ->
eval_expr def >>=
extend_env id >>+
eval_expr body
| ITE(e1,e2,e3) ->
eval_expr e1 >>=
bool_of_boolVal >>= fun b ->
if b
then eval_expr e2
else eval_expr e3
| IsZero(e) ->
eval_expr e >>=
int_of_numVal >>= fun n ->
return @@ BoolVal (n = 0)
| Proc(id,e) ->
lookup_env >>= fun en ->
return (ProcVal(id,e,en))
| App(e1,e2) ->
eval_expr e1 >>= fun v1 ->
eval_expr e2 >>= fun v2 ->
apply_proc v1 v2
| Abs(e1) ->
eval_expr e1 >>=
int_of_numVal >>= fun n1 ->
return @@ NumVal (abs n1)
| Cons(e1, e2) ->
eval_expr e1 >>= fun v1 ->
eval_expr e2 >>=
list_of_listVal >>= fun l2 ->
return @@ ListVal (v1::l2)
| Hd(e1) ->
eval_expr e1 >>=
list_of_listVal >>= fun l1 ->
if l1=[]
then error "Empty list"
else return @@ List.hd l1
| Tl(e1) ->
eval_expr e1 >>=
list_of_listVal >>= fun l1 ->
if l1=[]
then error "Empty list"
else return @@ ListVal (List.tl l1)
| Empty(e1) ->
eval_expr e1 >>= fun v1 ->
if is_listVal v1
then
return v1 >>=
list_of_listVal >>= fun l1 ->
return @@ BoolVal (l1 = []);
else
return v1 >>=
tree_of_treeVal >>= fun t1 ->
return @@ BoolVal (t1 = Empty);
| EmptyList ->
return @@ ListVal []
| EmptyTree ->
return @@ TreeVal Empty
| Node(e1,lte,rte) ->
eval_expr e1 >>= fun v1 ->
eval_expr lte >>=
tree_of_treeVal >>= fun t1 ->
eval_expr rte >>=
tree_of_treeVal >>= fun t2 ->
return @@ TreeVal (Node (v1, t1, t2))
| CaseT(target,emptycase,id1,id2,id3,nodecase) ->
eval_expr target >>=
tree_of_treeVal >>= fun targ1 ->
match targ1 with
| Empty -> eval_expr emptycase
| Node (v1,t1,t2) ->
fun env1 ->
eval_expr nodecase (ExtendEnv (id1, v1, ExtendEnv (id2, (TreeVal t1), ExtendEnv (id3, (TreeVal t2), env1))))
and
eval_prog (AProg e) = eval_expr e
(***********************************************************************)
(* Everything above this is essentially the same as we saw in lecture. *)
(***********************************************************************)
(* Parse a string into an ast *)
let parse s =
let lexbuf = Lexing.from_string s in
let ast = Parser.prog Lexer.read lexbuf in
ast
let lexer s =
let lexbuf = Lexing.from_string s
in Lexer.read lexbuf
(* Interpret an expression *)
let interp (e:string) : exp_val result =
let c = e |> parse |> eval_prog
in run c
Related Samples
Explore our OCAML Assignment Samples for clear, concise solutions to programming challenges. Enhance your understanding of functional programming, data structures, and algorithm design with practical examples tailored to educational needs. Perfect for students aiming to grasp OCAML concepts effectively and excel in their coursework.
OCaml
Word Count
12229 Words
Writer Name:Dr. Heather M. More
Total Orders:800
Satisfaction rate:
OCaml
Word Count
7510 Words
Writer Name:Priya Nair
Total Orders:841
Satisfaction rate:
OCaml
Word Count
20285 Words
Writer Name:Prof. Benjamin Tan
Total Orders:911
Satisfaction rate:
OCaml
Word Count
1057 Words
Writer Name:Dr. Brian G. Hernandez
Total Orders:600
Satisfaction rate:
OCaml
Word Count
6509 Words
Writer Name:Dr. Kristen R. West
Total Orders:700
Satisfaction rate:
OCaml
Word Count
32909 Words
Writer Name:Dr. Brian G. Hernandez
Total Orders:600
Satisfaction rate:
OCaml
Word Count
4490 Words
Writer Name:Prof. Liam Anderson
Total Orders:944
Satisfaction rate:
OCaml
Word Count
3696 Words
Writer Name:Prof. Benjamin Reynolds
Total Orders:711
Satisfaction rate:
OCaml
Word Count
2987 Words
Writer Name:Prof. William Johnson
Total Orders:748
Satisfaction rate:
OCaml
Word Count
3673 Words
Writer Name:Prof. William Johnson
Total Orders:748
Satisfaction rate: