Implementing recursive functions using ARM assembly in Keil homework help

The homework deals with implementing the solution to the Hanoi tower problem using ARM assembly. The program uses a recursive function to implement the solution. The function follows the ARM calling convention and saves the used registers on the stack. The number of required moves is calculated by the function and returned to the main program. The program is simulated on the Keil IDE. Here is the solution to demonstrate the quality of work delivered via our ARM assembly homework help service.

Using Recursive Functions to Solve Hanoi Tower Problem in Keil IDE

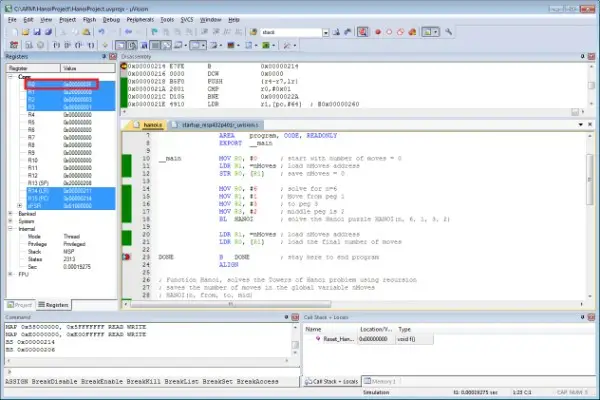
Source Code

Solution ; Program to solve the Towers of Hanoi problem for 6 disks AREA data, ALIGN=2 nMoves SPACE 4 GLOBAL __main AREA program, CODE, READONLY EXPORT __main __main MOV R0, #0 ; start with number of moves = 0 LDR R1, =nMoves ; load nMoves address STR R0, [R1] ; save nMoves = 0 MOV R0, #6 ; solve for n=6 MOV R1, #1 ; Move from peg 1 MOV R2, #3 ; to peg 3 MOV R3, #2 ; middle peg is 2 BL HANOI ; solve the Hanoi puzzle HANOI(n, 6, 1, 3, 2) LDR R1, =nMoves ; load nMoves address LDR R0, [R1] ; load the final number of moves DONE B DONE ; stay here to end program ALIGN ; Function Hanoi, solves the Towers of Hanoi problem using recursion ; saves the number of moves in the global variable nMoves ; HANOI(n, from, to, mid) HANOI PUSH {R4-R7, LR} ; save registers CMP R0, #1 ; if we are solving for 1 disk BNE HANOI_MOVE ; if it's not 1, make move LDR R1, =nMoves ; load nMoves address LDR R0, [R1] ; load current number of moves ADD R0, R0, #1 ; increment 1 move STR R0, [R1] ; update moves in variable B HANOI_RETURN ; return to caller HANOI_MOVE MOV R4, R0 ; save arguments in saved registers MOV R5, R1 MOV R6, R2 MOV R7, R3 SUB R0, R4, #1 ; pass n - 1 for call MOV R1, R5 ; pass same from value MOV R2, R7 ; pass old mid as to for call MOV R3, R6 ; pass old to as mid for call BL HANOI ; HANOI(n-1, from, mid, to) LDR R1, =nMoves ; load nMoves address LDR R0, [R1] ; load current number of moves ADD R0, R0, #1 ; increment 1 move STR R0, [R1] ; update moves in variable SUB R0, R4, #1 ; pass n - 1 for call MOV R1, R7 ; pass old mid as from value MOV R2, R6 ; pass old to as to for call MOV R3, R5 ; pass old from as mid for call BL HANOI ; HANOI(n-1, mid, to, from) HANOI_RETURN POP {R4-R7, LR} ; restore registers BX LR ; return to caller ALIGN END