Create Program to Implement A Function To Determine If A Number Is Prime, To Get Prime Factors Of A Number In SML Assignment Solution

Instructions

Objective

Write a program to create a program to create functions to determine if a number is prime, to get prime factors of a number in SML.

Requirements and Specifications

Install SML and make yourself familiar with it. The exercises in this assignment should help you get better acquainted with SML.

You are to submit code in SML as .sml files, with solutions to each exercise, which consist of providing implementations, in SML, to the following functions:

• factor(x,y) : boolean - returns true if x is a factor of y.
• prime(x) : boolean - returns true if x is prime.
• gcd(x,y) : int - computes the greatest common divisor for x and y.
• perfect(x) : boolean - returns true if x is a perfect number Links to an external site.
• amicable(x,y) : boolean - returns true if x and y are amicable numbers Links to an external site..
• occr(nums,x) : int - returns the number of times that x occurs in nums (which is an array (Ruby) or a list (SML)).
• primes(nums) : list or array of int - returns a list (or array) with prime numbers contained in nums.
• primeFactors(x) : list or array of int - returns a list (or array) containing the prime factors of x.

Screenshots of output

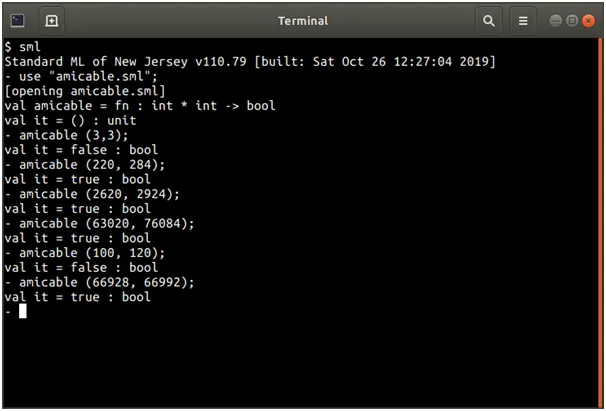
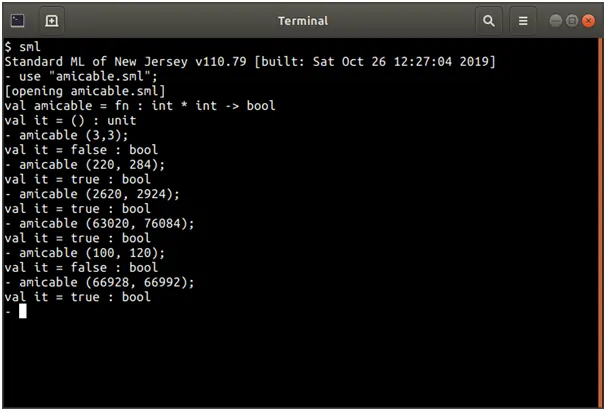
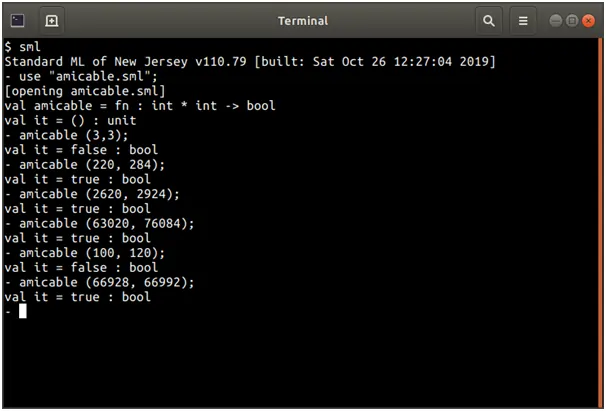
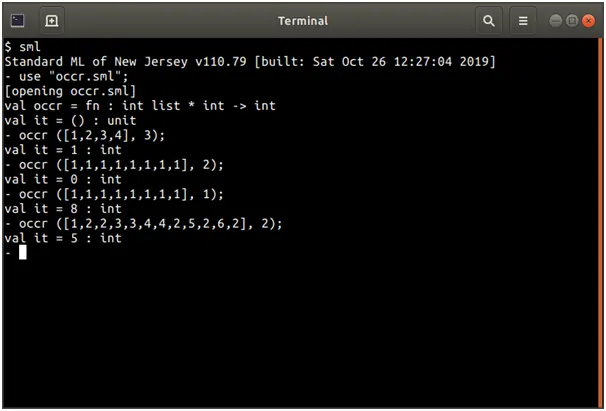
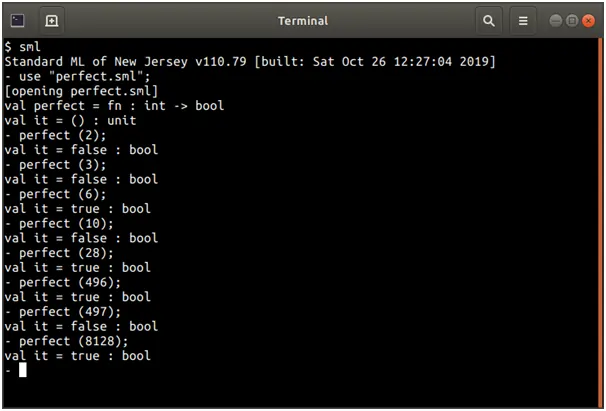
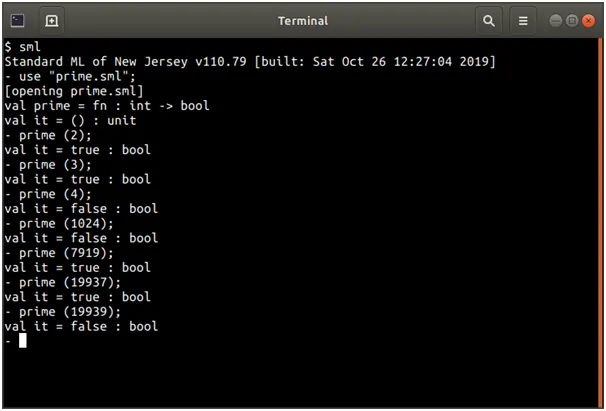
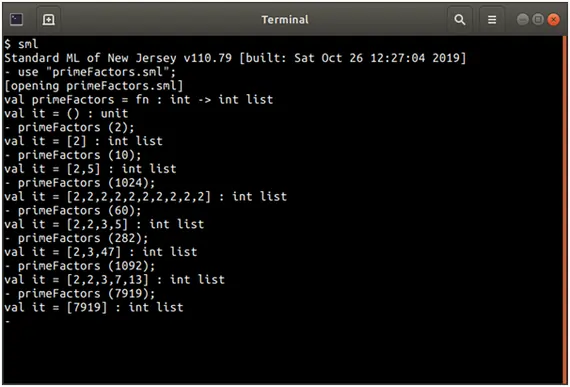
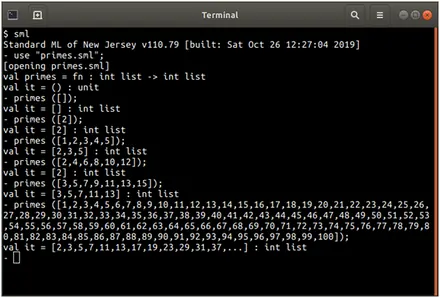
Source Code

Amicable.sml

(* Function amicable, returns true if x and y are amicable numbers *) fun amicable(x : int, y : int) : bool = let fun divisor_sum (n : int, sum : int) : int = if (n >= x) then sum else if (x mod n) = 0 then divisor_sum (n + 1, sum + n) else divisor_sum (n + 1, sum) in divisor_sum (1, 0) = y end

Factor.sml

(* Function factor, returns true if x is a factor of y *) fun factor(x : int, y : int): bool = (x mod y) = 0

Gcd.sml

(* Function gcd, computes the greatest common divisor for x and y *) fun gcd (x : int, y : int) : int = if (y = 0) then x else gcd (y, (x mod y))

Occr.sml

(* Function occr, returns the number of times that x occurs in nums (which is an array (Ruby) or a list (SML)). *) fun occr(nums : int list, x : int) : int = case nums of [] => 0 | (a :: ts) => (if (a = x) then 1 else 0) + occr (ts, x)

Perfect.sml

(* Function perfect, returns true if x is a perfect number *) fun perfect(x : int) : bool = let fun divisor_sum (n : int, sum : int) : int = if (n >= x) then sum else if (x mod n = 0) then divisor_sum (n + 1, sum + n) else divisor_sum (n + 1, sum) in divisor_sum (1, 0) = x end

Prime.sml

(* Function prime, returns true if x is prime *) fun prime (x : int) : bool = let fun is_divisor (n : int) : bool = if (n * n > x) then false else if (x mod n = 0) then true else is_divisor (n + 1) in if (x <= 1) then false else x = 2 orelse (not (is_divisor (2))) end

primeFactor.sml

(* Function primeFactors, returns a list (or array) containing the prime factors of x *) fun primeFactors(x : int) : int list = let fun get_divisors (n : int, x : int) : int list = if (n > x) then [] else if (x mod n = 0) then n :: (get_divisors(n, x div n)) else get_divisors (n + 1, x) in get_divisors (2, x) end