Calculate Function to Solve Anagrams and Calculate Perfect Numbers in a Haskell Assignment Solution

Instructions

Objective

Write a program to function to solve anagrams and calculate perfect numbers in a haskell assignment solution.

Requirements and Specifications

Problem 5.6 - define the function perfects that returns all perfect numbers up to and including a given limit.

A number is "perfect" if it is equal to the sum of its factors.

Fizzbuzz is a classic programming challenge were you must convert a sequence of integers to either the integer itself (as a string), the string "fizz" if the integer is divisible by 3, the string "buzz" if the string is divisible by 5, and "fizzbuzz" if the string is divisible by both 3 and 5. Implement fizzbuzz below, using an array comprehension on the sequence of integers 1 up to and including the given integer.

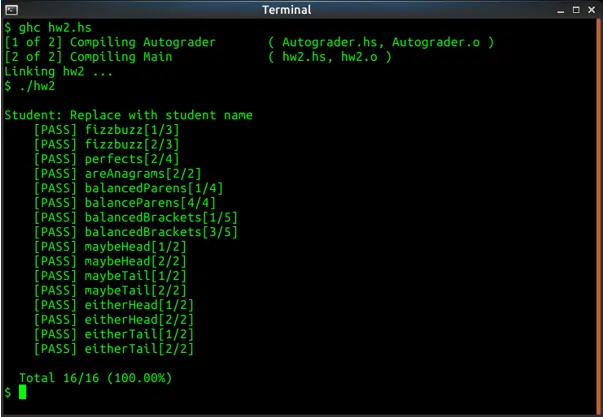
Screenshots of output

Source Code

module Main where import Autograder import Data.Map.Strict as Map -- imported to use Map in areAnagrams {- HW2 INSTRUCTIONS 1. Update the instance HW1 Solution name function to return your name (as it appears in ICON). 2. For each problem below, delete `undefined` and replace with your solution. If you need a helper function (hint: you probably will for a few of these), make sure it is limited to the context in which it is used. That is, do not create helper functions that are globally visible. -} instance HW2 Solution where -- TODO: Add your name here name a = "Replace with student name" -- You should not need to modify these perfectsSol a x = perfects x fizzbuzzSol a n = fizzbuzz n areAnagramsSol a s1 s2 = areAnagrams s1 s2 balancedParensSol a s = balancedParens s balancedBracketsSol a s = balancedBrackets s maybeHeadSol a xs = maybeHead xs maybeTailSol a xs = maybeTail xs eitherHeadSol a xs = eitherHead xs eitherTailSol a xs = eitherTail xs {- (P1) Problem 5.6 - define the function perfects that returns all perfect numbers up to and including a given limit. A number is "perfect" if it is equal to the sum of its factors. Ex. 1) factors 6 = [1, 2, 3], sum [1, 2, 3] = 6 therefore 6 is perfect Ex. 2) factors 28 = [1, 2, 4, 7, 14], sum [1, 2, 4, 7, 14] = 28 therefore 28 is perfect Ex. 3) factors 8 = [1, 2, 4], sum [1, 2, 4] = 7 therefore 8 is _not_ perfect Example evaluation of this function (from the book) perfects 500 = [6, 28, 496] -} -- ********** perfects :: Integral b => b -> [b] perfects m = Prelude.filter perfect [3..m] where perfect n = sum (getFactors n) == n -- is perfect if sum of factors equals the number getFactors n = [i | i <- [1..(n `div` 2)], n `mod` i == 0] {- (P2) Fizzbuzz is a classic programming challenge were you must convert a sequence of integers to either the integer itself (as a string), the string "fizz" if the integer is divisible by 3, the string "buzz" if the string is divisible by 5, and "fizzbuzz" if the string is divisible by both 3 and 5. Implement fizzbuzz below, using an array comprehension on the sequence of integers 1 up to and including the given integer. -} fizzbuzz :: (Integral b, Show b) => b -> [String] fizzbuzz n = [if (zmod i 3) || (zmod i 5) then (fb i 3) ++ (fb i 5) else (show i) | i <- [1..n]] where fb m x | x == 3 && (zmod m 3) = "fizz" | x == 5 && (zmod m 5) = "buzz" | otherwise = "" zmod a b = (a `mod` b) == 0 {- (P3) Determine if two strings are anagrams. Hint: use Haskell's Data.Map.Strict data structure -} areAnagrams :: String -> String -> Bool areAnagrams s1 s2 = isAnagram s1 (fromList (zip s2 s2)) where isAnagram [] m = Map.null m isAnagram (x:xs) m = if member x m then isAnagram xs (delete x m) else False {- (P4) Given a string of parentheses, determine if they are balanced. ()() -> balanced (True) ((()())) -> balanced (True) )( -> unbalanced (False) ())() -> unbalanced (False) -} balancedParens :: String -> Bool balancedParens xs = balanced xs [] where balanced [] xs = Prelude.null xs -- no chars in input, no pending closings balanced (x:xs) ys | x == '(' = balanced xs (')':ys) -- add pending closing and recurse with tail -- remove one pending closing and recurse with tail | otherwise = if Prelude.null ys || (head ys) /= x then False else balanced xs (tail ys) {- (P5) Similar to [[balancedParens]], but this time the input can contain parentheses, curly brackets, and square brackets. ()[]{} -> balanced (True) ({}[]) -> balanced (True) ([)] -> unbalanced (False) ([[]) -> unbalanced (False) -} balancedBrackets :: String -> Bool balancedBrackets xs = balanced xs [] where balanced [] xs = Prelude.null xs -- no chars in input, no pending closings balanced (x:xs) ys | x == '(' = balanced xs (')':ys) -- add pending closing and recurse with tail | x == '{' = balanced xs ('}':ys) -- add pending closing and recurse with tail | x == '[' = balanced xs (']':ys) -- add pending closing and recurse with tail -- remove one pending closing and recurse with tail | otherwise = if Prelude.null ys || (head ys) /= x then False else balanced xs (tail ys) {- (P6) Implement the function maybeHead so that it returns a Maybe containing either the head of the list if it exists, otherwise Nothing. -} maybeHead :: [a] -> Maybe a maybeHead [] = Nothing maybeHead (x:xs) = Just x {- (P7) Implement the function maybeTail so that it returns a Maybe containing either the head of the list if it exists, otherwise Nothing. -} maybeTail :: [a] -> Maybe [a] maybeTail [] = Nothing maybeTail (x:xs) = Just xs {- (P8) Implement eitherHead so that it returns an Either containing the head of the list if it exists, otherwise a string describing the error. -} eitherHead :: [a] -> Either String a eitherHead [] = Left "empty" eitherHead (x:xs) = Right x {- (P9) Implement eitherTail so that it returns an Either containing the tail of the list if it exists, otherwise a string describing the error. -} eitherTail :: [a] -> Either String [a] eitherTail [] = Left "empty" eitherTail (x:xs) = Right xs main = do let s = Student "Your name here" autograde s