Calculate Energy Demand of Charging Electric Vehicles In Haskell Assignment Solution

Instructions

Objective

Write a program to calculate energy demand of charging electric vehicles in Haskell.

Requirements and Specifications

Screenshots of output

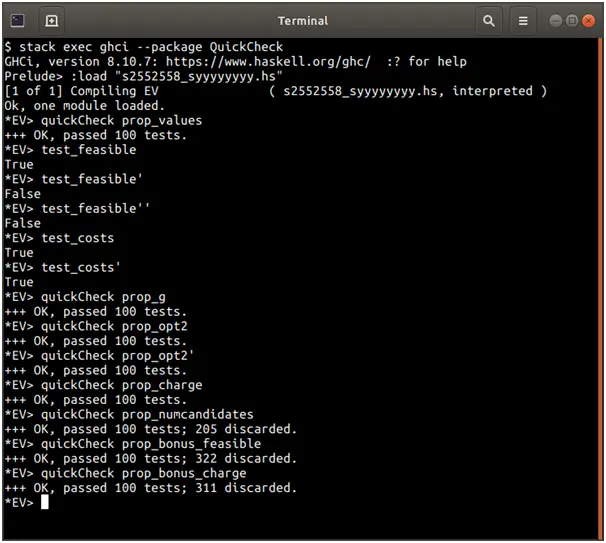
Source Code

module EV where -- !!!!IMPORTANT!!!! Don't include more modules ("imports"): it's not needed and the grading would fail :( !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! import Test.QuickCheck -- Testing is used to spot problems early. Note, that testing can only be used to find problems, but it cannot show that your solution is correct! import Data.List -- For 'subsequences' import Data.Tuple -- For 'swap', in case you need it import Data.Char {- If you want to provide feedback or comment, please leave it here. Unfortunately, we will not see the Canvas comments. ------------------------------------------------------------------------------ ... ------------------------------------------------------------------------------ -} infix 4 ~= -- This makes Profile a synonym for [(Int, Double)], i.e., you can interchange Profile and [(Int, Double)], they mean the same type Profile = [(Int, Double)] epsilon = 0.001 -- !!!!! DO NOT CHANGE ANYTHING ABOVE THIS LINE !!!!! ------------------------------------------------------------------------------ -- Your information -- ------------------------------------------------------------------------------ -- Add your student numbers. If this is missing, your results will not end up in the administration. -- Only add students who contributed to this assignment and should receive a result. studentnumber1 :: String studentnumber1 = "s2552558" studentnumber2 :: String studentnumber2 = "syyyyyyy" -- If you work alone, leave this line unchanged, otherwise the grading fails. -- Please add your names here studentname1 :: String studentname1 = "Renato Chavez Chicoma German" studentname2 :: String studentname2 = "Name" -- If you work alone, leave this line unchanged, otherwise the grading fails. ------------------------------------------------------------------------------ -- QUESTION 1+2a+2b -- ------------------------------------------------------------------------------ (~=) :: Double -> Double -> Bool x ~= y = abs(x-y) <= epsilon -- replace undefined by your solution (for Question 2a) -- For Question 1, you need to use this function. Nothing needs to be handed in a = 1 - 1/3 ~= 2/3 -- Change this as requested in the assignment (Question 2b) b = (sqrt 2) ^ 2 ~= 2 -- Change this as requested in the assignment (Question 2b) ------------------------------------------------------------------------------ -- QUESTION 3 -- ------------------------------------------------------------------------------ idx :: [Double] -> Profile idx xs = zip [1..] xs -- replace this line by your own definition ------------------------------------------------------------------------------ -- QUESTION 4 -- ------------------------------------------------------------------------------ values :: Profile -> [Double] values xs = map snd xs -- replace this line by your own definition -- 'idx' and 'values' cancel eachother. You can test your functions with: quickCheck prop_values prop_values xs = values (idx xs) == xs ------------------------------------------------------------------------------ -- QUESTION 5 -- ------------------------------------------------------------------------------ expand :: (Int, Int) -> Profile -> Profile expand (n, m) [] = zip [n..m] (repeat 0) expand (n, m) ((i,x):xs) | i == n = (n, x) : expand (n + 1, m) xs | otherwise = (n, 0) : expand (n + 1, m) ((i,x):xs) -- add helper functions here -- ^^^^^^^^^^^^^^^^^^^^^^^^^^ ------------------------------------------------------------------------------ -- QUESTION 6 -- ------------------------------------------------------------------------------ feasible :: Double -> Profile -> Bool feasible c xs = sum (values xs) ~= c && all (>=0) (values xs) -- add helper functions here -- ^^^^^^^^^^^^^^^^^^^^^^^^^^ test_feasible = feasible 2.0 (idx [1,0,1]) -- Should give True test_feasible' = feasible 2.0 (idx [1,0,0]) -- Should give False test_feasible'' = feasible 2.0 (idx [-1,0,3]) -- Should give False ------------------------------------------------------------------------------ -- QUESTION 7 -- ------------------------------------------------------------------------------ costs :: Profile -> Profile -> Double costs ps xs = sum (map (\(x, y) -> (x + y)^2) (zip (values ps) (values xs))) ------------------------------------------------------------------------------ -- QUESTION 8: test if it works, you do not need to change/submit anything -- ------------------------------------------------------------------------------ -- This helps you to verify 'costs' for two examples, just evaluate it (it should give 'True'). Make sure that you understand the calculation below, this could help when implementing 'costs' test_costs = costs (idx [1,2,3]) (idx [3,2,1]) ~= (1+3)^2 + (2+2)^2 + (3+1)^2 test_costs' = costs (idx [4,0]) (idx [1,2]) ~= (4+1)^2 + (0+2)^2 ------------------------------------------------------------------------------ -- QUESTION 9 -- ------------------------------------------------------------------------------ -- The function 'f' from the pearl assignment description. Make sure you understand it, since 'g' is implemented similarly. f :: Double -> Double -> Double -> Double -> Double -> Double f x1 x2 c p1 p2 = (p1+x1)^2 + (p2+x2)^2 -- Don't change this, it is correct :-) g :: Double -> Double -> Double -> Double -> Double g x1 c p1 p2 = (p1+x1)^2 + (p2+x2)^2 where x2 = c - x1 -- Use this property to test your function 'g' for common mistakes prop_g x1 x2 p1 p2 = f x1 x2 c p1 p2 ~= g x1 c p1 p2 where c = x1 + x2 ------------------------------------------------------------------------------ -- QUESTION 10: -- ------------------------------------------------------------------------------ -- You do not need to hand in anything for Question 10. But if you do -- not check this, the later exercises may become very difficult and -- the TAs may ask for your notes on this exercise. -- Ask for help if you do not know how to proceed ------------------------------------------------------------------------------ -- QUESTION 11: -- ------------------------------------------------------------------------------ -- You do not need to hand in anything for Question 11. But if you do -- not check this, the later exercises may become very difficult and -- the TAs may ask for your notes on this exercise. -- Ask for help if you do not know how to proceed ------------------------------------------------------------------------------ -- QUESTION 12 -- ------------------------------------------------------------------------------ -- Provide the derivative of 'g' here g' :: Double -> Double -> Double -> Double -> Double g' x1 c p1 p2 = 4*x1 + 2*(p1 - p2) - 2*c ------------------------------------------------------------------------------ -- QUESTION 13 -- ------------------------------------------------------------------------------ opt2 :: Double -> Double -> Double -> (Double, Double) opt2 c p1 p2 = (x1, c - x1) where x1 = (p2 - p1 + c) / 2 -- Checks if at the optimal x1 the derivative g' is zero prop_opt2 c p1 p2 = g' x1 c p1 p2 ~= 0 && x1+x2 ~= c where (x1,x2) = opt2 c p1 p2 -- If we are at the optimal point, this means that moving away from it gives higher costs prop_opt2' c p1 p2 = f (x1+0.1) (x2-0.1) c p1 p2 >= f x1 x2 c p1 p2 && f (x1-0.1) (x2+0.1) c p1 p2 >= f x1 x2 c p1 p2 where (x1,x2) = opt2 c p1 p2 ------------------------------------------------------------------------------ -- QUESTION 14 -- ------------------------------------------------------------------------------ -- You do not need to hand in anything for Question 14. But if you do -- not check this, the later exercises may become very difficult and -- the TAs may ask for your notes on this exercise. -- Ask for help if you do not know how to proceed ------------------------------------------------------------------------------ -- QUESTION 15 -- ------------------------------------------------------------------------------ proof :: String proof = "induction" ------------------------------------------------------------------------------ -- QUESTION 16 -- ------------------------------------------------------------------------------ charge :: Double -> Profile -> Profile charge c ps = let cs = csum c ps in map (\(i, p) -> (i, cs - p)) ps -- add helper functions here -- Calculate the value: C + Sum (pi) / N csum c ps = (c + sum (values ps)) / genericLength ps -- ^^^^^^^^^^^^^^^^^^^^^^^^^^ -- For N=2, 'charge' and 'opt2' should give the same answer. If it does not match, either one of the two functions has a problem. Also check prop_opt2 and prop_opt2' prop_charge c p1 p2 = x1 ~= x1' && x2 ~= x2' where [x1, x2 ] = values $ charge c (idx [p1,p2]) (x1',x2') = opt2 c p1 p2 ------------------------------------------------------------------------------ -- QUESTION 17 -- ------------------------------------------------------------------------------ -- If you do not know how to solve this, try 'candidates' with a profile that contains only zero's and determine its length. Do you see a pattern and can you explain it? numcandidates :: Int -> Int numcandidates n = 2^n - 1 ------------------------------------------------------------------------------ -- QUESTION 18 -- ------------------------------------------------------------------------------ candidates :: Double -> Profile -> [Profile] candidates c ps = [expand (m, n) chg | chg <- [charge c ss | ss <- subsequences ps], feasible c chg] where m = fst (head ps) n = fst (last ps) -- add helper functions here -- ^^^^^^^^^^^^^^^^^^^^^^^^^^ -- The candidates for the profile with only zeros are always feasible when the candidate covers >0 intervals. Count if this matches 'numcandidates'. prop_numcandidates (Positive n) = n > 0 && n < 16 ==> length (candidates 100 (idx $ replicate n 0)) == numcandidates n {------------------------------------------------------------------------------- -- BONUS -- -------------------------------------------------------------------------------} ------------------------------------------------------------------------------ -- QUESTION 19 -- ------------------------------------------------------------------------------ -- Below you can add your helper functions for the bonus optimalevcharging c ps = snd (minimum (map (\cd -> (costs cd ps, cd)) (candidates' c ps))) candidates' :: Double -> Profile -> [Profile] candidates' c ps = [expand (m, n) chg | chg <- [charge c ss | ss <- tail $ subsequences ps], feasible c chg] where m = fst (head ps) n = fst (last ps) ------------------------------------------------------------------------------ -- Some tests that may help you while working on the bonus -- ------------------------------------------------------------------------------ -- If the following quickCheck tests do not pass, most likely you made a mistake. -- Test if 'optimalevcharging' always produces a feasible solution. Should always take just a few seconds. Increase 15 to 150 if you want to check longer profiles. prop_bonus_feasible (Positive c) (NonEmpty ps) = length ps' < 15 ==> feasible c xs where xs = optimalevcharging c ps' ps' = idx ps -- Test if 'optimalevcharging' charges according to 'charge' when it charged (note: this does not guarantee it is optimal). Should always take just a few seconds. Increase 15 to 150 if you want to check longer profiles. prop_bonus_charge (Positive c) (NonEmpty ps) = length ps < 15 ==> and $ zipWith (~=) subprofile subxs where ps' = idx ps xs = optimalevcharging c ps' subprofile = [ x | (i,x) <- xs, x > 0] subps = [ (i,p) | ((i,x),(j,p)) <- zip xs ps', i==j, x > 0] subxs = values $ charge c subps